H.R. Suiter著 「Star Testing astronomical telescopes」の紹介(ver.0)
2014年4月 舟越 和己
ここでは、Star Testingの本に載っていることの主なポイントを簡単に紹介します。
■本の構成

1994年に初版(現在は第2版が出ている)。初版の目次は下記のように全15章から成っています;
第1章 序論
第2章 スターテストマニュアル要約
第3章 望遠鏡はフィルターです
第4章 回折
第5章 スターテストを行うこと
第6章 光軸不一致
第7章 大気のゆらぎと筒内気流
第8章 締め付けとたわみのある光学系
第9章 遮蔽と遮光
第10章 球面収差
第11章 円形ゾーンとターンエッジ
第12章 色収差
第13章 ラフネス(Roughness)
第14章 非点収差
第15章 蓄積された光学系の問題
→第1章では、天体望遠鏡の光学精度の例や波面収差の定義などが書かれています。
第2章はスターテストで重要なポイントとなる「焦点内外像」の特徴を要約した内容です。
第3章は望遠鏡をオーディオシステムと比較し、本書の説明で重要な概念となるMTFについて
書かれています。
第4章は光の回折現象の説明です。
第5章はスターテストを行うために必要な条件(人工星の設置条件など)とスターテストの実施例です。
第6章から14章までは個々の問題について詳細にスターテストでの判別法や対処法が述べられて
います。
第15章は上記の複合的な問題を扱います。
(内容的に難しい箇所は第4章Fresnel Zoneの話、第7章のフラクタルの話、及び10章の一般的収差関数
の話です。
■Star Testingの本で重要な3つの項目;
下記の3つが6章以降で詳細に議論されます。
(1)焦点内外像 (2)MTF (3)収差関数(理想波面(注)と収差のある波面(注)との差の関数)
(注)Star testingの本では、「波面(wavefront)」については既知であるとして話が進むので、この意味
を知らない人は下記等を参考に理解して下さい;
http://www.cybernet.co.jp/codev/lecture/optics/opt01/
■Star Testとは?
この本では次のように説明しています;
・スターテストは、より正確には”点光源”テストと命名されるものです。
・スターテストで要求されることは、良質の高倍率用アイピースと、(テストに)都合良く位置した星、
又は照らされたピンホール、そしていくらかの経験です。
・スターテストは、多くの場合、星である点光源の焦点上の像及び焦点の両側の像(これを焦点
内外像という)を確かめます。
・焦点内外像は収差のユニークな表現を”明らかに”しています。特に、焦点から外れた環状の像
は焦点から内側と外側で同じ距離を少し外した所で同じように現れますが、それは光学系が優秀な
ときのみです。
■「第1章 序論」のポイント
●天体望遠鏡の表面精度について
・「天体望遠鏡の対物の許容誤差は金属切断旋盤の通常の正確さよりも数千倍小さい値です。」
→非常に高精度!
・この具体的な例として、下記が示されています;
「20cmの望遠鏡のミラーを1.6kmまで拡大したとする。通常の厚さの比率なら、拡大されたミラーの
厚さは268m。このスケールでは黄緑の光(550nm)の波長λ=4.4mm(注1)。従って、表面の光学的
許容誤差の最大値は僅かλ/8=0.55mm。高品質な光学系では0.25mm以下。
→これは直径1.6kmで高さが268mの巨大円板の表面の許容誤差がトランプ1枚の厚さ(約0.3mm)
しかないことを示している(注2)!(人間により作られた最も正確な固い表面)」
(注1) 1nm(ナノメートル)=0.000001mmなので20cmから1.6kmに拡大のスケールでは
λ=550*0.000001*1600/0.2=4.4m
(注2)上の例の1.6kmまで拡大されたミラーがどのくらい巨大かを参考のためエアーズロックや東京タワー
と比較してみました;

●波面収差の表し方
(1)PーV波面収差(peak-to-valley wavefront error)とは?
・レンズを通過した実際の波面は、理想波面に較べて偏差があります。これは、実際の波面が理想波面
に対して波打っているのでずれのピークと谷があります。このピークと谷の差、つまり理想波面とのずれ
の最大値をピークから 谷までの偏差(山から谷までの偏差)と呼び、 PーV波面収差と言います。
PーV波面収差をトータル波面収差とも言います。
(2)RMS波面収差とは?
RMSはroot mean square(平均自乗平方根)の略です。実際の波面と理想波面には多かれ少なかれ
至る所で偏差があります。RMS波面収差は、この偏差を標準偏差で表したものです。
(参考)下記はRMS波面収差の分かり易い説明図です(フランスの一般向け天文書より)
http://astrophotography.fr/olt/p2b.jpg
この図では、波面収差を基準からの偏差で色分けしています(赤は+の偏差、青は-の偏差など)。
また、RMS=146nm, P-V(PTV)=850nm, 平均(moyenne)=50nmという値が波面収差の横断面の例として
示されています。この横断面から分かるように、P-V値は波面収差の最も高い値(ピーク)と最も低い値
(谷底)との差です。
(3)PーV波面収差とRMS波面収差の関連
一般に、PーV波面収差=λ/4 ⇔ RMS波面収差=λ/14の対応があると言われます。
(Star Testing:P.7)すなわち、近似的には下記となります;
PーV波面収差≒3.5×RMS波面収差
(注)Star Testingの第10章では、もう少し細かく次のように述べています;
「RMS値からPV値を導くためには、近似的に13.4/4の因子を掛けなければなりません:
1/4波長(山から谷)=1/13.4波長(RMS)」(Star Testing: P.172)
●波面精度のルール(レイリーのルール)
「もし全体の波面誤差(頂上から谷)が黄緑の光(550nm)の1/4波長を越えるならば、その光学系は
明らかなデグレードが始まる。」
→従って、P-V波面収差が1/4波長以内であれば、その光学系は回折による制限のみを受けた像質
(ディフラクション・リミテッド)に達すると言われます。又これを、1/4波長のレイリー許容誤差
(Rayleigh tolerance)と言います。
●ストレールレシオ
光学的品質の評価によく使われるものとして、ストレールレシオ(Strehl ratio)があります。これは、ディフ
ラクションリングのセントラルスポット(最も明るい部分:エアリーディスクとも言う)に集まる光の強度と無
収差の光学系のセントラルスポットに集まる光の強度との比のことです。一般に、ストレール・レシオ=
0.8(80%)の値に達した場合、その光学系は、回折のみの制限をうける(ディフラクションリミテッドに達す
る)。これは、λ/4レイリー許容誤差、すなわち1/4波長の品質に相当します。
●RMS波面収差とストレール・レシオの関係;
ストレール・レシオ(V)≒1-(2π×RMS波面収差)2
●下記の(1)から(4)の表現は全て同じ1/4-波長(1/4λ)の品質を表しています;
(1) 1/8-波長の表面(1/8-wavelength surface);
→反射鏡の場合は、入射と反射の2回があるので、1/4λの品質となるための許容誤差はλ/8
必要となります。
(2) ±1/16-表面(±1/16-wave surface);
→反射鏡の場合、もし同じ1/8波長のこぶが底から頂上までを測られなく、その平均の位置から測ら
れるならば、誤差は ±1/16となる。
(3)1/27-波長のRMSの表面(1/27-wave RMS on the surface);
→これは光学産業界で広く使われているメジャーで、マレシャルの評価基準 (Marechal‘s criterion)と
して知られている。(1/4波長(山から谷)=1/13.4波長(RMS)より)
(4) He-Neレーザー光による1/31-波長のRMSの表面精度 (1/31-wave RMS He-Ne laser light
surface accuracy);
→ヘリウム-ネオンレーザーの赤い光は長い波長(633nm)のためレイリー基準の黄緑の光(550nm)に
比べて誤差は小さく現れます(1/(27*(633/550))=1/31)。
●波面精度を単一の数値で表現する限界
・P-V波面精度は表面の山と谷の差がしきい値(例えば1/4λ)以内にあれば良いということしか要求
してないので、山と谷のスロープが滑らかどうかはP-V波面精度では正確には分かりません。
・RMS波面収差も標準偏差なので山と谷のスロープが滑らかどうかは正確には分かりません。
●光学品質を示す最も完璧な方法は?
・それは、詳細な変調伝達関数(MTF: modulation transfer function)を示すことです。これは、光学シス
テムがいろいろな間隔のバーのパターンのコントラストを保つ能力のことです。どんな光学的な難点も
MTFから逃れることはできません。
■「第2章 スターテストマニュアル要約」のポイント
●回折像と焦点内外像に関する用語
・focused:焦点が合った。
・out-of-focus:焦点から外れた。
この他にStar Testingでは次の用語が登場します;
・inside focus:焦点内側。焦点よりも前の位置。
・outside focus:焦点外側。焦点よりも後ろの位置。
●焦点内外像の特徴
・合焦装置を内側、外側に進めるとき、溝が中央に現れ、水に落ちた小石から広がる波紋のように
外側に動きます。
・焦点内側のディスクは焦点外側のディスクに近似的に同一です。もし、両サイドのパターンが似て
いて、それらが円形ならば、その光学系は完全に近くなります。
・しかし、収差など問題のある光学系はこの完全性を破壊します。アイピースを焦点の内外に動かす
ことにより、望遠鏡を乱している問題を探し、特定することができます。
●望遠鏡の光学的問題(3つのタイプ)
1.光学システムのベースライン特性
(a)光学経路の副鏡の遮蔽。
(b)鏡の前のスパイダー羽やミラークリップのブロック。
(c)透過の変動(ぼかして不完全なコーティング)。
(d)レンズの屈折における色の変化
2.一時的、又は修理可能な問題
(a)光学エレメントの光軸不一致、又は異常な傾き。
(b)大気の揺らぎの効果。
(c)望遠鏡の近く又は内部の温度差の影響。
(d)(薄いミラーの締め付けやたわみのような)光学エレメントの通常でない歪み。
(e)ミラーやレンズの上のほこりや汚れ。
3.ガラスのエラー
(a)球面収差(波面が球面に適合できないこと)。
(b)荒れた光学表面(セントラルスポットから散乱した光の原因となる)。
(c)ゾーン(ガラスのディスクのターンダウンエッジを含む鏡の軽度の丸い丘や溝)。
(d)収色差(補正されていない色のエラー)。
(e)非点収差(軸に沿う像の一様でない拡り)
第2章では、これらのエラーの主なものについて、スターテストのメインである「焦点上の像及び焦点
の両側の像」の概要が内外像と一緒に説明されています(ここでは省略);
・副鏡の遮蔽 ・光軸不一致 ・大気の動きと揺らぎ ・筒内気流 ・光学系の締め付け又はたわみ
・球面収差 ・荒れた表面 ・輪帯収差 ・ターンエッジ ・非点収差
→第2章での上記の説明はあくまでも概要レベルで、それらの詳細は6章以降に書かれています。
■「第3章 望遠鏡はフィルターです」のポイント
●オーディオとの比較
光学系のフィルタリングの概念をサウンドシステムとのアナロジーで対比すると、
フィルター フィルター
(望遠鏡/眼/カメラ) (サウンドシステム)
・開口の直径 ・スピーカーのサイズ
・色付きのフィルター ・イコライザーのフィルター
・画像処理 ・信号処理
・散乱した光 ・オーディオのノイズ
・空間応答 ・周波数応答
(原著P.39のTable 3-1より)
第3章では、上記の項目毎にその対比が説明されています(ここでは省略)。この中で最も重要な項目
は「空間応答」です。これはMTF(Modulation Transfer Function)と関連します。
●空間周波数とは?
・オーディオ機器などの特性評価として周波数特性があります。これは原音に対する、
[マイクロフォン→録音・再生回路→スピーカー]
による再生音の忠実度を表すものです。特に高忠実度のものはハイファイ(high fidelityの略)と
呼ばれています。
・レンズも同様に「光学信号の伝達系」と考えた場合、光学系の周波数特性が測定できれば、光学
信号が忠実に伝達されているかどうかを知ることができます。レンズでいう周波数とは、1mm幅の中
に正弦的に濃度の変化するパターンが何本あるかという意味で特に「空間周波数」と呼ばれ、電気
系のHzに対し、「○○line per mm」あるいは「○○本/mm」と示されます。すなわち、空間周波数
とは、像面上で1ミリあたりの白黒パターンの本数のことです。
また、単位角度(1秒角)内に数えられる明暗のサイクル数を「空間周波数」ということもあります。
・倍率を上げると空間周波数は大きくなりますが、空間周波数の最大値Smaxは、望遠鏡の口径と
観測する光の波長により決まります;
Smax=D/λ[サイクル/radian]=(D/λ)*(π/180)*(1/3600)[サイクル/秒角]
(例)D=100mm,λ=550/1000000mmの場合、
Smax=182000[サイクル/radian]=0.88[サイクル/秒角]
●空間周波数の最大値と分解能の関係
Smax=D/λの逆数をθminとすると、これは与えられた光学系の最大分解能を意味している(明暗
を分離できる最小の幅を意味するので)。すなわち、θmin=1*λ/Dである。
これをよく知られている望遠鏡の分解能と比較すると、
・レイリーリミット(2つのエアリー;ディスクの中心がちょうど半径だけ離れている)
θ=1.22*λ/D
→従って、ディフラクションディスクの半径に等しいバーの分離は最大空間周波数の1/1.22=0.82
で生じます。
・ドーズ・リミット(レイリー・リミットより85%中心が接近)
θ=0.85*1.22*λ/D=1.037*λ/D
→従って、ドーズ・リミットでの分離は最大空間周波数の1/1.037=0.97で生じます。
●Modulationとは?
対象物の明暗のコントラストの度合いを示す値をModulationと云い、下記の式で表します。
Modulation=(I(明)-I(暗))/(I(明)+I(暗))
Modulationの値が大きいほどコントラストが高い。最もコントラストが高いときModulation=1.0となり、
最もコントラストが低いときModulation=0となります。
●光学系によるModulationの変換
・対象物のModulationを光学系にインプットした場合、出力されるModulationはどうなるかを見ます。
光学システムの変換関数は常にそのコントラストを減少させるように働きます。従って光学系による
Modulationの変換はその値を減少させる方向に向かいます。
●最大空間周波数のフラクション(割合)
空間周波数の最大値Smax=D/λを1.0に正規化したときの最大空間周波数を「最大空間周波数の
フラクション(Fraction ofmaximum spatial frequency)」と云います。
→このとき、「空間周波数の最大値と分解能の関係」で述べたように最大空間周波数のフラクション
のスケールで下記のことが示されます;
・Smax=1.0
・レイリーリミット=0.82
・ドーズリミット=0.97
●MTF(Modulation Transfer Function)とは?
・MTFとは、最大空間周波数のフラクションを変数とするModulationのtransfer関数のことです。
横軸に最大空間周波数のフラクション、縦軸にModulationのtransfer値を取りグラフ表現されます。
→Star Testingの本ではMTFのグラフが各章で使用されます。
◆(参考)MTFを理解するための良い解説資料(英文)
・Cloudy Nightsの2011年のスレッドに「How to understand an MTF chart...(MTFチャートの理解の
仕方...)」というのがあります。非常に長文の投稿ですがMTFの具体的な例を説明しています。
http://www.cloudynights.com/ubbthreads/showflat.php/Cat/0/Number/4415334/page/0/view/collap
sed/sb/5/o/all/fpart/all/vc/1
→これの解説は、Cloudy NightsのMTFの話題紹介を参照下さい。
・Telescope Optics: Evaluation and Design by Harrie Ruttenの第18章も分かり易い内容です。
■「第4章 回折」のポイント
この章は内容が難しいので原著の4.1節の部分のみポイントを紹介します。
●光の回折の特徴
1. 回折は光の波という性質により生じます。光は局所化できないので、像は必然的にファジーと
なります。フォトンを粒子とする量子力学の考えもその位置を決めることにはなりません。
2. 回折は制限された開口の結果です。それは機器の焦点を決める能力とは独立な角度のぼかし
です。
3.回折は単にリングに見られる現象だけではありません。セントラルスポットの広がりは回折により
生じます。
4.回折は境界を提供する開口を持つ定常波としてモデル化できるので、準静的な(quasi-static)
明と暗の領域が存在します。
5.光学品質には越えるのが難しい限界があります。
ひとたび回折の実際上の知識を持ったら、スターテストを理解するのが容易になります。回折の
概念のいくつかは物理学で最も美しく基本的なものです。」(原著P.55より)
●現代の量子論と光の回折について
Star Testingの本では、現代の量子論が回折現象をどう説明しているかを次のように紹介しています;
「量子革命は光がフォトンと呼ばれる離散的な粒子のパッケージであるということを明らかにしました。
・・・・しかし量子論は奇妙で直感的ではありません。それを理解するために、我々は、我々の巨視的
な世界の経験を進んで破棄しなければなりません。量子力学において、フォトンの位置をそれが検出
される前に記述できる方法は、その確率密度、すなわち特定の位置でフォトンと遭遇する可能性を与
えることです。」(原著P.58, P.59より)
→Star Testingではこの文章の後に、この原理を説明する実験が紹介され、フォトンの振舞がハイゼン
ベルグの不確定性原理によりおおまかに説明されます。そして、最後にエアリーディスクの半径が求め
られます。このあたりは原著P.61に書かれています。
■「第5章 スターテストを行うこと」のポイント
この章では下記の内容が話題になっています;
1. デフォーカス(defocus)と焦点深度の話。
2. 人工光源の大きさ、作り方、置き方。
3. ”公式の”スターテストの準備と手順。
●デフォーカスとは?
・結像点からの光軸方向へのずれで、「焦点ズレ」とも言います。
・合焦装置によりアイピースを焦点から前後に動かすことにより発生します。
●デフォーカスの量と焦点深度
・デフォーカスの量はアイピースの動きという直接的な方法ではなく、「開口絞りの波面で測定され
た値」を使用します。その理由は、この値が望遠鏡のタイプを横断する普遍的な値だからです。
開口絞りの波面で測定されたデフォーカス値がλ/4の波面の差となる焦点のズレを「焦点深度」
と言います(この範囲内の焦点ズレは望遠鏡の性能にレイリーの意味で影響しない。焦点ズレの
許容範囲)。
●人工光源がスターテストとして選ばれる理由:
1.ある程度、明るさをコントロールすることができる。
2.明るい光源により、フィルターを使用して色を変えたり、調節したりすることができる。
3.接近したテストは、大気の動揺の介入を少なくする。
4.光源は望遠鏡に関し固定されているので星を追跡する必要がない。
一方、人工光源にはいくつかの欠点があります:
1.人工星の使用は水平な望遠鏡の位置を要求し、この位置は光学セルに通常でない非点収差や
光軸の不一致、及び「たわみ」はセルの垂直な位置からもたらされるかもしれない。
2.人工光源の推奨距離のいくつかは1600フィート(約0.5km)離れて見ることを要求している(非常に
長い距離が必要な場合がある)。
3.(人工源は)点のような光源にするために、望遠鏡の解像度よりも小さくなるようにピンホールの
直径を知る必要がある。
●人工光源までの距離
天体は無限遠の距離にあると考えてよいので、近くの光源でテストした時に十分に機能した望遠鏡は、
遠くの空に向けたときにはうまくいきません(それは球面収差として現れます)。
→では、どのくらい人工光源を離さないといけないのでしょうか? この本では、光源がどのくらい近づく
と受け入れられない過修正の球面収差が現れるかを示す「Roger Sinnottの式」が紹介されています。
●人工星の直径
直径を決める方針が述べられています;
・スターテストを行うためには、人工光源のピンホールのサイズは機器の解像力よりも小さくなるように
注意深く選択しなければなりません。
・一方、それは焦点外の像を光で満たすのに十分な明りになるくらい大きくなければなりません。
・この直径を計算するためには、ピンホールの遠方にエアリーディスクの半径を拡大し、その半径
が光源のピンホールの直径として選ばれるならば、光源は点像の角度の広がりの半分に過ぎない
ということになります。
●反射球の使用
人工光源は、ピンホールという小さな光源の製作に成功しても、それにランプやフラッシュを付け、
小さな穴を通る光に焦点を合わせなければなりません。
これに代わる容易なものとして、小さな球状の反射体による太陽の煌めきを使用することが、必要な
小さいサイズと光の強度を達成する優れた方法として紹介されています。
●スターテストの手順
5章の最後に、スターテストの手順が述べられています;
(1)テストに必要な光源までの距離を求める。
↓
(2)テストに必要な光源のサイズを求める。
↓
(3)光源のサイズから必要な反射球のサイズを求める。
↓
(4)上記の(1)~(3)からテスト環境を設置する。
↓
(5)各種のスターテストを実施する。
そして、4種類の仮想的な望遠鏡に対する具体的なテスト手順と結果(スターテスト結果とアセスメント)
が記述されています。例えば、8インチf/6ニュートン式反射のテスト結果とアセスメントでは、下記の
ようになっています;
<テスト結果>
1.光軸が合っているか。→OK
2.(光学系の)締め付けや非点収差がないか。→OK
3.高倍率を使用して、合焦装置を焦点の前後に動かす「スナップテスト」
→OK(明確な焦点に素早く変わる)
4.球面収差の確認→負修正の球面収差有(ダイアゴナルの影が中心に等しく現れる合焦点装置
の動きの平均比率が1:2又は1:3)
5.輪帯収差→確認できない(タイトな円形構造は見られない)
6.ターンエッジ→確認できない
<アセスメント>
「この望遠鏡は惑星に普通に使用可だが、あまり良くない。しかしメーカーに不満を言う程ではない。
光学系はひどく荒れていないが、鏡面の荒れのテストは暗い視野と大気の安定が必要。結論として
この望遠鏡は一般的な目的で使用される能力は持っている。」
■「第6章 光軸不一致」のポイント
この章では下記の内容が話題になっています;
1. 光軸不一致の影響。
2. 光軸不一致の収差関数。
3.光軸不一致のMTF。
4. 3種類の望遠鏡の光軸修正手順。
●光軸不一致の影響
光軸不一致が悪化すると、非点収差がコマを圧倒し主要な収差になります。コマはコリメーション
エラーを線形的に悪化させるのに対し、非点収差は光軸からの外れの距離の二乗として増大し
ます。コマと非点収差のグラフの交差点は「粗い光軸一致」のレベルでは生じません。すなわち、
ニュートン式望遠鏡で光軸不一致の場合、コマは非点収差よりも強く現れます。
●光軸不一致の収差関数
収差関数とは理想波面と収差のある波面との差を表現する関数です。光軸不一致でミラーが傾いて
いる場合、(理想波面-光軸不一致の波面)は、片側で -、もう一方側で+となります。したがって、
光軸不一致の収差関数のシミュレーションでは、波面の差はちょうど中心を外して強打した太鼓の
皮のようです。片方の半円は下の方に変形し、他方の半円は上の方に底を上げてバランスを取って
います。
■「第7章 大気のゆらぎと筒内気流」のポイント
この章では下記の内容が話題になっています;
1.屈折媒体としての大気の話
2.大気の揺らぎと収差関数
3.大気の揺らぎに起因するMTF
4.大気の揺らぎの観察と修正のアクション
5.筒内気流と収差関数
6.筒内気流のMTF
7.筒内気流の観察と修正のアクション
→ここでは、フラクタルによる大気の揺らぎのモデルについてのみ紹介します。
この部分は、原書では文章による説明が中心なのでイメージが掴みにくいところです。
それでここでは、簡単な場合の例を図により説明します。
●大気の揺らぎで乱れた波面とその数理的表現
星からの光は大気層に入る前は平坦な波面ですが、大気層を通して望遠鏡の開口に到達したとき
は、気圧や温度が一様でない ことに起因する「乱れた波面」になります。
→この波面を数理的に表現する手法として「フラクタル」が適用できます。
●大気の揺らぎの準解析的手順としてフラクタルが適用された経緯;
波面の統計的偏差は通常、準解析的手順で扱われます。ランダム偏差に対してガウス形式(=正規
分布)を仮定しているこれらの手順は長時間露出のMTFや荒れた表面に関係する性質を計算する
ために非常に有効です(Schroeder 1987, P.315)。しかし、それらは単一の像の見え方を計算する
ことはできません。それらは荒れた開口のような多くの点の平均化された振舞です。波面をシミュ
レーションするために使用される手法は中点変位のフラクタルアルゴリズムと呼ばれるものです。
それは素晴らしいフラクタルな景観を生成するために使用されます。それはまた、開口を通過した
直後の人工的な疑似ランダム波面を与えることができます。(Star Testing原文P.131,132)
●フラクタル(fractale)とは?
・フラクタルは、フランスの数学者ブノワ・マンデルブロ(1924-2010)が導入した幾何学の概念。
・図形の部分と全体が自己相似になっているものをいう。即ち、その図形の一部として、図形全体と
相似な形を含むような図形です。
●中点変位法(midpoint displacement)とは?
フラクタル図形を作る手法の一つです。直線の場合で説明します。
線分の両端をP, Qとし、その中点のZ方向への変位を下記により求めます;
中点の変位=(両端の点P, QのZ方向の偏差平均)+Δz=(z1+z2)/2 +Δz
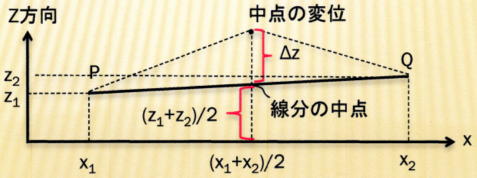
ここでΔzは「ランダムな偏差(乱数で求める増減)」です。中点変位法によりフラクタル図形を作る
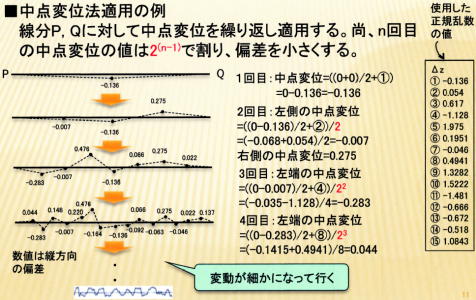
ためには、線分P, Qに対して中点変位を繰り返し適用します。尚、n回目の中点変位の値は2(n-1)
で割り、偏差を小さくします。
◆ランダムなΔzの作り方→コインを投げて「裏と表が出る確率」は、共に二分の一です。
コインを投げて表が出た場合に点を線分の中点より上に1進め、裏が出た場合に
点を線分の中点より下に1進める試行を行います(これを1次元のランダムウォーク
という)。これを無限回繰り返した場合に、点がある位置xに存在する確率は正規分布
になります。
上記の内容を図により説明すると、次のようになります;
●中点変位法の適用
大気の揺らぎの波面のシミュレーションは、「中点変位法」を平面に対して適用して行います。
その手順の概要は下記です;
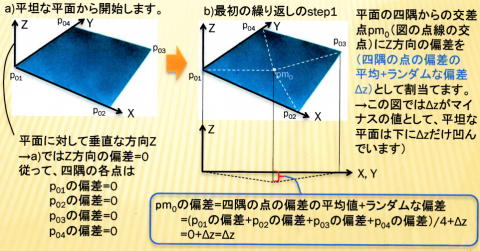
a)平坦な平面から開始します。
→平面のZ方向の偏差=0従って、平面の四隅の各点はp01の偏差=0, p02の偏差=0,
p03の偏差=0, p04の偏差=0の状態から開始します。
b)最初の繰り返しのstep1;
→平面の四隅からの交差点pm0にZ方向の偏差を
(四隅の点の偏差の平均+ランダムな偏差Δz)
として割当てます。pm0の偏差=四隅の点の偏差の平均値+ランダムな偏差
=(p01の偏差+p02の偏差+p03の偏差+p04の偏差)/4+Δz=0+Δz=Δz
a), b)を図示すると、次のようになります;
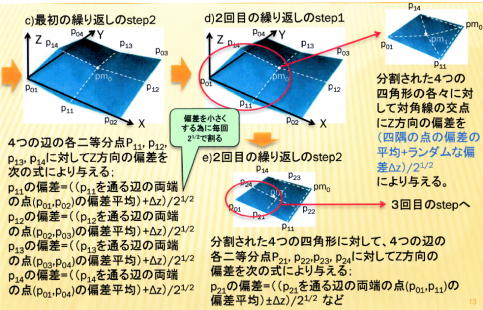
c)最初の繰り返しのstep2;
→4つの辺の各二等分点P11, p12,p13, p14に対してZ方向の偏差を次の式により与えます;
・p11の偏差=((p11を通る辺の両端の点(p01,p02)の偏差平均)+Δz)/21/2
・p12の偏差=((p12を通る辺の両端の点(p02,p03)の偏差平均)+Δz)/21/2
・p13の偏差=((p13を通る辺の両端の点(p03,p04)の偏差平均)+Δz)/21/2
・p14の偏差=((p14を通る辺の両端の点(p01,p04)の偏差平均)+Δz)/21/2
d)2回目の繰り返しのstep1;
→分割された4つの四角形の各々に対して対角線の交点にZ方向の偏差を
(四隅の点の偏差の平均+ランダムな偏差Δz)/21/2
により与えます。
e)2回目の繰り返しのstep2;
→分割された4つの四角形に対して、4つの辺の各二等分点P21, p22,p23, p24に対してZ方向の
偏差を次の式により与える;
p21の偏差=((p21を通る辺の両端の点(p01,p11)の偏差平均)±Δz)/21/2 など
c), d), e)を図示すると、次のようになります;
以降、3回目のstep1, step2,・・・, n回目のstep1, step2と繰り返していくと、自己相似形が段々細か
になって行きます。Star Testingの本では7回の繰り返しを行います。
自己相似形が段々細かくなっていく様子を図示すると、次のようになります;

●中点変位法による大気の揺らぎモデルの問題点と対策
しかし、以上のような非物理的な数学的手順での構成にはいくつかの問題があります。
・中点変位のフラクタルでは、同じようなスケール(サイズ)のランダムな偏差が繰返し現れます。
・一方、大気の揺らぎでは、ランダムな偏差のスケール、または気流の変化間の距離は2から20cm
のオーダーにあり、平均見積は10cm程度です
→この理由により、中点変位のアルゴリズムは少し修正され、各段階の除数は21/2ではなく、(2q)1/2
となります。ここでqは抑制因子です。qが1より大のとき、アルゴリズムの波面は細かいスケールの
荒れが圧縮され、粗い偏差(長い偏差)が目立つように柔らかくなります。ここで使用される抑制因子
は1.1と1.6の間です。このような抑制因子で生成された像は、自己類似性は失われますが実際の
大気の揺らぎに近くなります。
→下の波面になります。

■「第8章 締め付けとたわみのある光学系」のポイント
この章では下記の内容が話題になっています;
1.原因
2.収差関数
3.締め付けられた光学系のMTF
4.締め付けられた光学系の回折パターン
→説明省略
■「第9章 遮蔽と遮光」のポイント
この章では下記の内容が話題になっています;
1.中央遮蔽
2.スパイダーの回折
3.遮光とアポダイゼーション
4.光学系の埃とひっかき傷
→ここでは、3の遮光とアポダイゼーションについて簡単に説明します。
●アポダイゼーションとは?
開口の透過性質を変更し回折リングを弱めるために使用されます。しかし、その代償として
エアリーディスクは肥大します。
ここで議論する開口の透過性質の変更とは、下の図のように「開口の中心では光の完全な通過」
を行い、「開口の縁に近くなるにつれて徐々に光の通過を減少させることです。
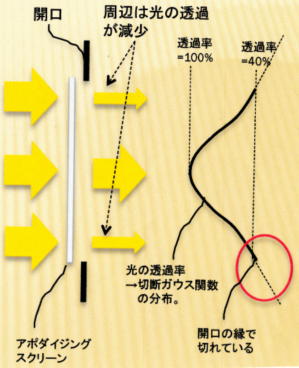
●切断ガウス関数とは?
上記の図のような「減少する遮光された光量の分布」は、正規分布が使われま正規分布関数は
ガウス関数とも呼ばれます。切断(truncated)という言葉は、この関数が開口の縁でカーブが切断
されているためです。切断ガウス関数は、開口の広さとカーブの傾きにより決まります(下図参照);
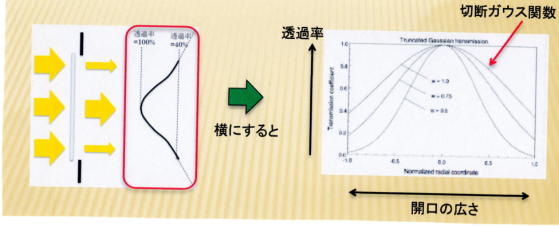
切断ガウス関数を使った遮光を「切断ガウス遮光」と言います。
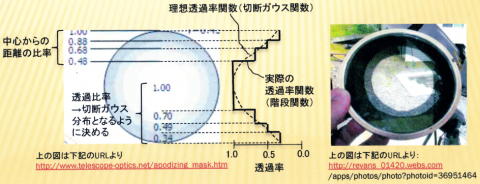
●アポダイゼーション実現の具体例
アポダイジングスクリーンは下記のように透過率が周辺に行くほど低下するように網目を数枚重ねて
作ります。このとき、透過率の分布は切断ガウス関数の近似関数として階段状の関数になります。
■「第10章 球面収差」のポイント
この章では下記の内容が話題になっています;
1.球面収差とは何か?
2.ハッブル宇宙望遠鏡
3.一般化された球面収差
4.収差関数
5.低次の球面収差と修正のためのテスト
6.高次の球面収差
7.光学品質のための基準
8.許容可能なエラー
→ここでは、1と3についてのみ簡単に紹介します。
●球面収差とは何か?
理想光学系を通過した波面は縮小する球面波面(理想波面)です;
・星からの光の波面は平行な平面の波面として望遠鏡の開口に到達します。
・理想光学系を通過した波面は、焦点に収束する同心球面の波面として進みます。
しかし、これは「理想の光学系」の話であり、実際には、焦点の前又は後に集る光が存在するケース
があります。このように、光線がレンズ(又はミラー)の中心を通るか、周辺部を通るかによって、異なる
位置で集光するために起きる収差を「球面収差」と言います。球面の断面をもつレンズ(又はミラー)に
は必ず球面収差が出ます。この場合、周辺の光線がレンズ(又はミラー)に近い所で交わります。
●球面収差のタイプ:負修正と過修正
・負修正:周辺の光線が中央の光線よりも対物(ミラー)側に近いところで交わるタイプの球面収差。
・過修正:周辺の光線が中央の光線よりも対物(ミラー)側から遠いところで交わるタイプの球面収差。
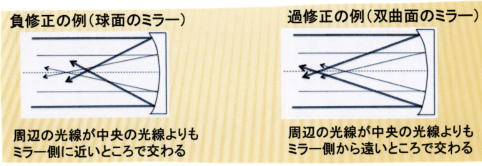
ニュートン式反射では過修正ミラーは双曲面」
●一般化された球面収差
ここでは光学系を通過した波面に着目します。すなわち、
「スターテストの観点からは、光学的表面の形状について考えたり、それらの長い名前を思い出す必要
はありません。光学系を通過した波面が完全な球面から差し引かれたときの形状についてのみ考えて
下さい。この差異は単純な多項式関数の形式に展開されます:
W(ρ) = A0 + A2ρ2 + A4ρ4+A6ρ6· · ·,
ここでρは0から1の範囲の動径座標です。記号W(ρ)は焦点を中心とする球から離れた波面のトータ
ルの歪みを表します。(Star Testing P.173)」
→「光学系を通過した波面が完全な球面から差し引かれたときの形状についてのみ考えて下さい。」
とは、
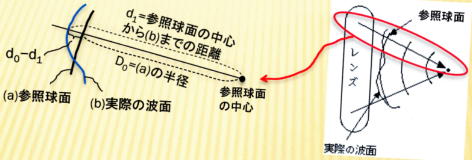
(a)焦点に収束する完全な球の波面=参照球面(reference sphere)
(b)光学系を通過した波面=実際の波面
として、その差分((a)の半径d0ー参照球面の中心から(b)までの距離d1)を考えることです。そして
この差分(d0ーd1)が上記の多項式関数の形式に展開されるということです。
これを図示すると、次のようになります;
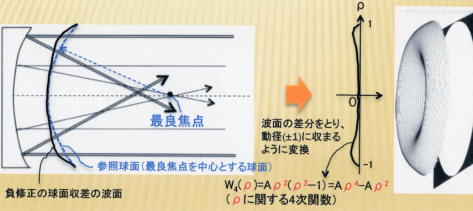
・ρに関する4次関数で表される球面収差を「低次の球面収差」と言います。
→球面収差関数が4次関数となる理由を負修正の場合に図示すると、次のようになります。
・これに対し、6次関数として表される球面収差を「高次の球面収差」と言います。
高次の球面収差は多くの望遠鏡において、少しの差しかなく、いくつかの特別な機器(例えば、
シュミットの補正版の形状)の問題と考えることができます。
→以上第10章までです。